
Derivative of log x base a modernpsado
Here you will learn differentiation of log x i.e logarithmic function by using first principle and its examples. Let's begin - Differentiation of log x (Logarithmic Function) with base e and a (1) Differentiation of log x or l o g e x: The differentiation of l o g e x, x > 0 with respect to x is 1 x. i.e. d d x l o g e x = 1 x

Ex 5.5, 7 Differentiate the function (log x)^x + x^log x
Show Solution Example: Using Properties of Logarithms in a Derivative Find the derivative of f (x) =ln( x2sinx 2x+1) f ( x) = ln ( x 2 sin x 2 x + 1) Show Solution Try It Differentiate: f (x)= ln(3x+2)5 f ( x) = ln ( 3 x + 2) 5. Hint Show Solution Watch the following video to see the worked solution to the above Try It.

Question Video Using Logarithmic Differentiation to Differentiate a
Derivative of y = ln u (where u is a function of x). Unfortunately, we can only use the logarithm laws to help us in a limited number of logarithm differentiation question types. Most often, we need to find the derivative of a logarithm of some function of x.For example, we may need to find the derivative of y = 2 ln (3x 2 − 1).. We need the following formula to solve such problems.

07 Differentiation of log x to the base a by first principle
Show Solution So, as the first example has shown we can use logarithmic differentiation to avoid using the product rule and/or quotient rule. We can also use logarithmic differentiation to differentiate functions in the form. y =(f (x))g(x) y = ( f ( x)) g ( x) Let's take a quick look at a simple example of this.
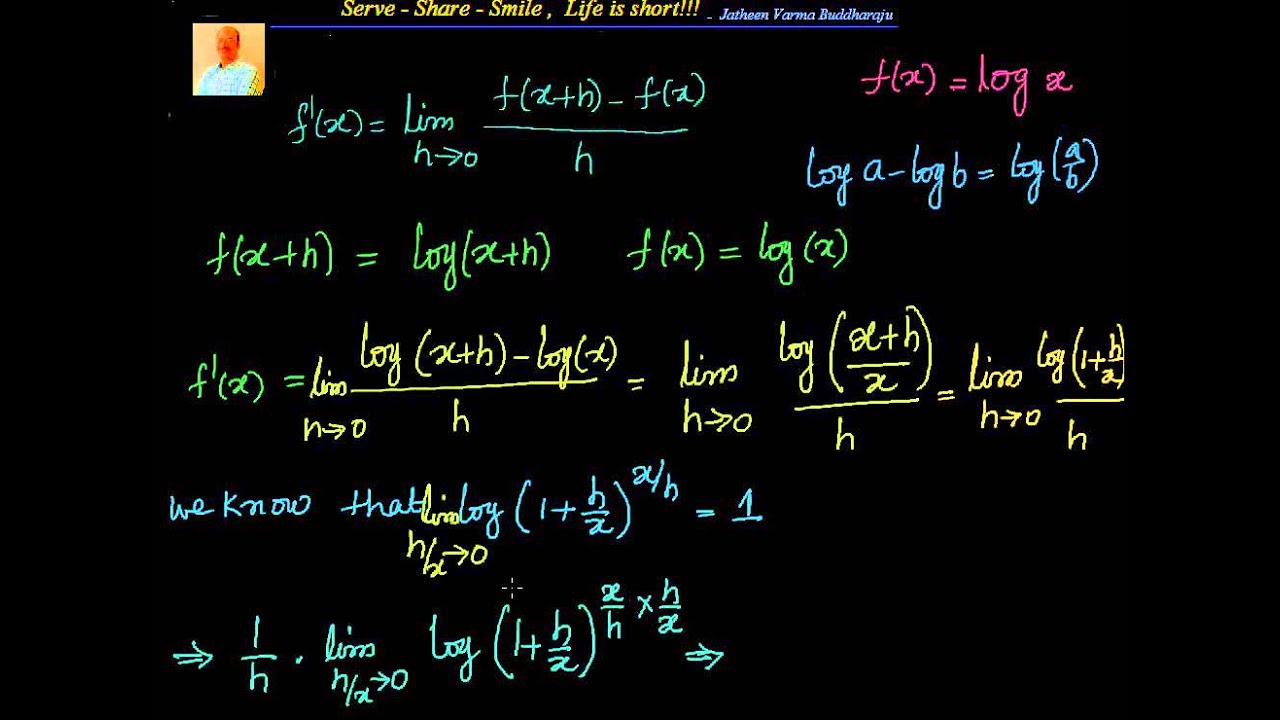
Calculus Differentiation Derivative of log x YouTube
Differentiation of Logarithmic Functions Examples of the derivatives of logarithmic functions, in calculus, are presented. Several examples, with detailed solutions, involving products, sums and quotients of exponential functions are examined. First Derivative of a Logarithmic Function to any Base The first derivative of f (x) = log b x is given by

Derivatives of Logarithmic Functions (Fully Explained!)
These functions require a technique called logarithmic differentiation, which allows us to differentiate any function of the form \(h(x)=g(x)^{f(x)}\). It can also be used to convert a very complex differentiation problem into a simpler one, such as finding the derivative of \(y=\frac{x\sqrt{2x+1}}{e^x\sin ^3x}\). We outline this technique in.
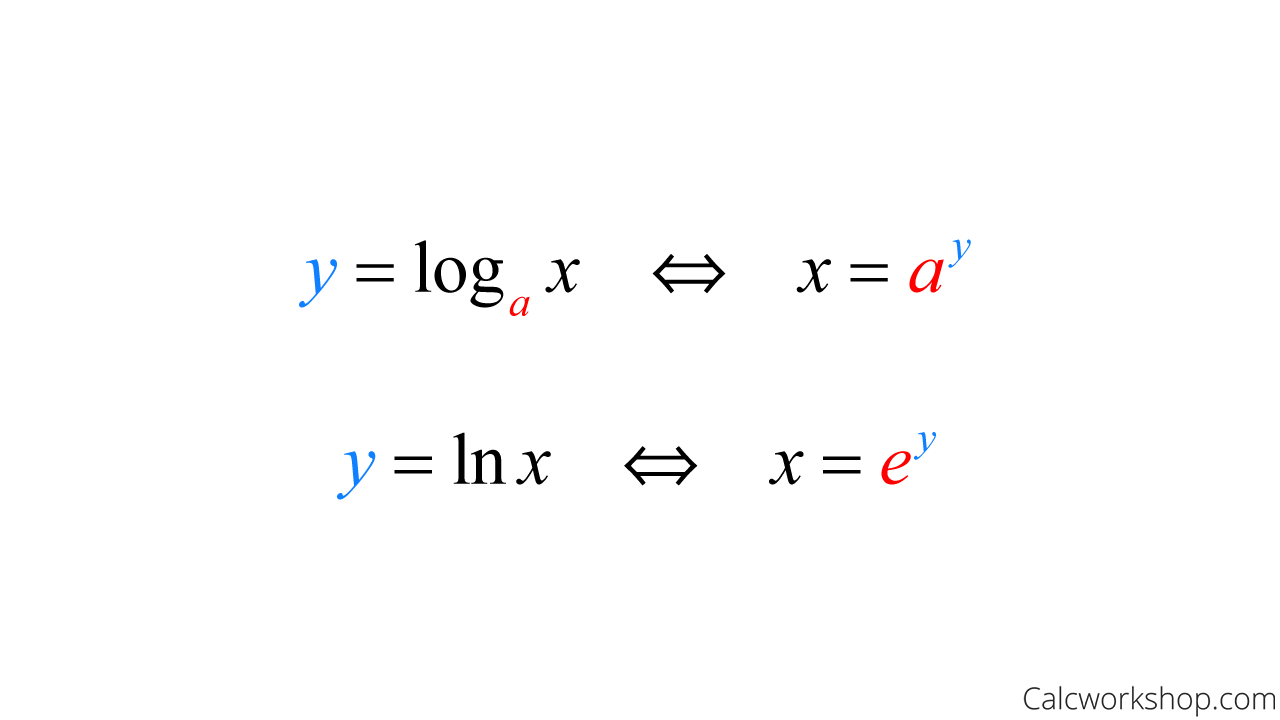
Logarithmic Function Formula
Solution: Given function: \ (\begin {array} {l}y = e^ {x^ {4}}\end {array} \) Taking natural logarithm of both the sides we get, ln y = ln e x4 ln y = x 4 ln e

Ex 5.5, 7 Differentiate the function (log x)^x + x^log x
This calculus video tutorial provides a basic introduction into derivatives of logarithmic functions. It explains how to find the derivative of natural loga.

Example 31 Derivative of a^x Chapter 5 Class 12 Logarithmic Diff
Solution 1: Use the chain rule. Let f (x) = \ln x f (x) = lnx and g (x) = 5x g(x) = 5x. Then we are asked to find ( f \circ g ) ' (f ∘g)′. Using chain rule, we know that ( f \circ g ) ' = ( f' \circ g) \times g' . (f ∘g)′ = (f ′ ∘g)×g′.

Ex 5.7, 9 Find second order derivatives of log (log x)
Mathematics Standard Formulae - 1 What is the d. Question What is the derivative of log ( x)? Solution Find the derivative of log ( x). Let, y = log ( x) Differentiate both sides w.r.t x d y d x = d d x log x = 1 x ∵ d d x log x = 1 x Therefore, the derivative of log ( x) is 1 x. Suggest Corrections 76 Similar questions Q.
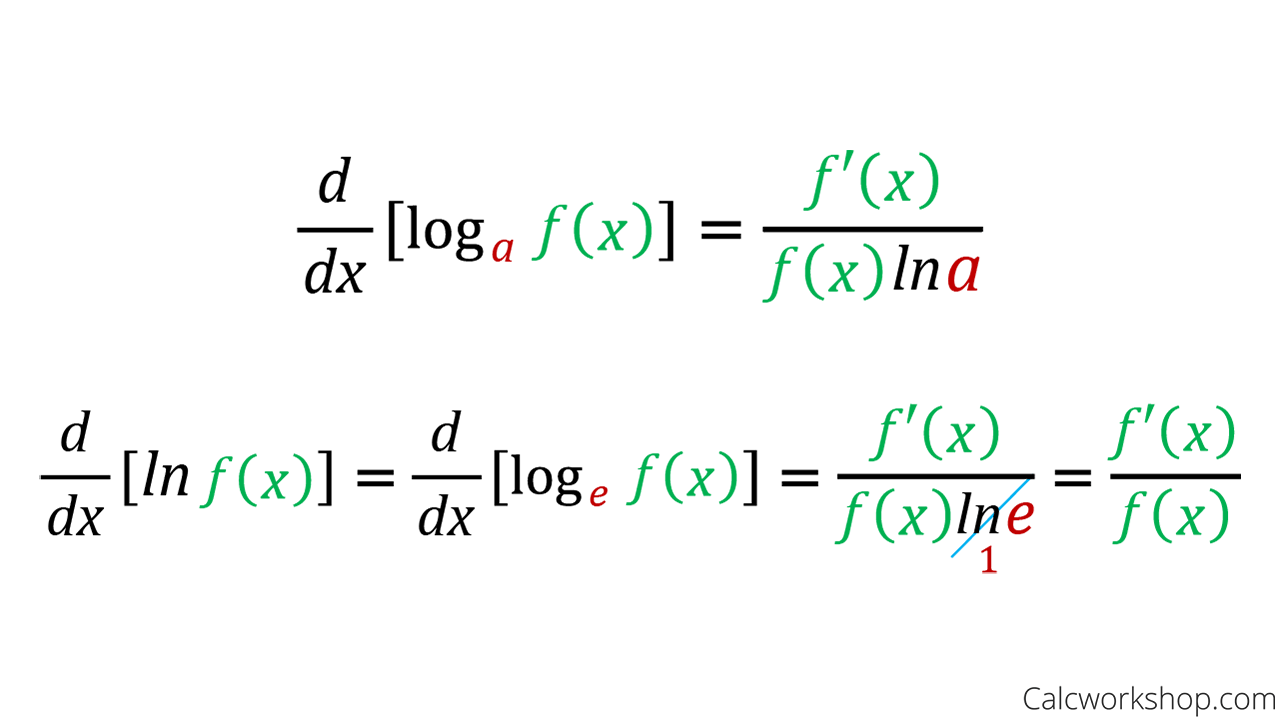
Derivatives of Logarithmic Functions
Free derivative calculator - differentiate functions with all the steps. Type in any function derivative to get the solution, steps and graph

Second derivative of log x clubsdase
Logarithmic differentiation is based on the logarithm properties and the chain rule of differentiation and is mainly used to differentiate functions of the form f(x) g(x)· It helps in easily performing the differentiation in simple and quick steps. The functions which are complex and cannot be algebraically solved and differentiated can be differentiated using logarithmic differentiation.

Differentiation of log (log x) Chain Rule Teachoo Ex 5.4
How do I differentiate logarithmic functions? First, you should know the derivatives for the basic logarithmic functions: d d x ln ( x) = 1 x d d x log b ( x) = 1 ln ( b) ⋅ x Notice that ln ( x) = log e ( x) is a specific case of the general form log b ( x) where b = e . Since ln ( e) = 1 we obtain the same result.

Ex 5.7, 4 Find second order derivatives of log x Teachoo
3.6: Derivatives of Logarithmic Functions. Page ID. As with the sine, we do not know anything about derivatives that allows us to compute the derivatives of the exponential and logarithmic functions without going back to basics. Let's do a little work with the definition again: d dxax = lim Δx → 0ax + Δx − ax Δx = lim Δx → 0axaΔx −.

Ex 5.5, 7 Differentiate the function (log x)^x + x^log x
more. By the change of base formula for logarithms, we can write logᵪa as ln (a)/ln (x). Now this is just an application of chain rule, with ln (a)/x as the outer function. So the derivative is -ln (a)/ ( (ln (x))²)· (1/x). Alternatively, we can use implicit differentiation: given y=logᵪ (a), we write x^y=a.
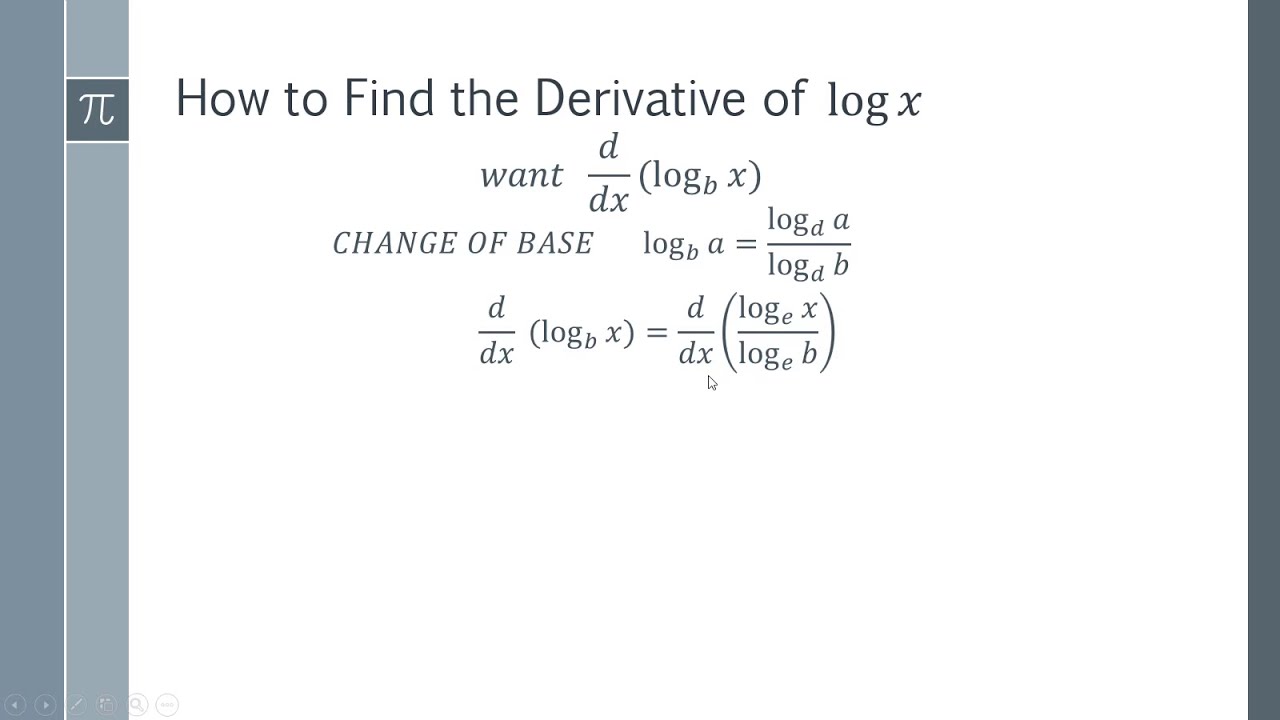
How to find the derivative of logx YouTube
Derivatives in maths enable the calculation of function change rates in terms of variables. The function defined by y = loga(x) ( x > 0) where x = ay, a > 0, a ≠ 1 is called the logarithm of x to the base a. The derivative of loga(x) is 1 xln ( a). The derivative of loga(x) is denoted by d dx(loga(x)) or (loga(x)).